Adição
Adição é uma das operações básicas da álgebra. Na sua forma mais simples,adição combina dois números (termos, somandos ou parcelas), em um único número, a soma. Adicionar mais números corresponde a repetir a operação. Por extensão a adição de 0, um ou um número infinito de números pode ser definida, veja abaixo.
Para uma definição da adição no âmbito dos números artificiais
Pode também ser uma operação geométrica - a partir de dois segmentos de recta dados determinar um outro cujo comprimento seja igual à soma dos dois iniciais.
Subtração
Subtração é uma operação matemática que indica quanto é um valor numérico (minuendo) se dele for removido outro valor numérico (subtraendo).
Uma subtração é representada por:
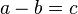
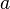 é o minuendo,
é o minuendo,  é o subtraendo e
é o subtraendo e  é a diferença ou resto.
é a diferença ou resto.
A subtração é o mesmo que a adição por um número de sinal inverso. É, portanto, a operação inversa da adição.
[EDITAR]PROPRIEDADES IMPORTANTES
- Fechamento: A diferença de dois números reais será sempre um número real.
- Elemento neutro: O número 0 (zero) não altera a diferença, em qualquer posição. Assim, x - 0 = x, y - 0 = y, e x - 0 - y = x - y, sendo x diferente de y.
- Anulação: Quando o minuendo é igual ao subtraendo, a diferença será 0 (zero).
Multiplicação
Em matemática, a multiplicação é uma operação binária. Na sua forma mais simples a multiplicação é uma forma simples de se adicionar uma quantidade finita de números iguais. O resultado da multiplicação de dois números é chamado produto. Os números sendo multiplicados são chamados de coeficientes ou operandos, e individualmente de multiplicando e multiplicador[1].
(lê-se "x vezes y" ou "y adicionado x vezes")
Assim, por exemplo,
Há controvérsias entre os educadores, sobre que número deveria normalmente ser considerado como o número de termos e qual o valor de cada termo.
Pode também ser uma operação geométrica - a partir de dois segmentos de reta dados determinar um outro cujo comprimento seja igual ao produto dos dois iniciais (veja aqui).
- Comutatividade: A ordem dos fatores não altera o resultado da operação. Assim, se x . y = z, logo y . x = z.
- Associatividade: O agrupamento dos fatores não altera o resultado.(Podemos juntar de dois em dois de modo que facilite o cálculo). Assim, se (x . y) . z = w, logo x . (y . z) = w.
- Distributividade: Um fator colocado em evidência numa soma dará como produto a soma do produto daquele fator com os demais fatores. Assim, x . (y + z) = (x . y) + (x . z).
- Elemento neutro: O fator 1 (um) não altera o resultado dos demais fatores. O um é chamado "Elemento neutro" da multiplicação. Assim, se x . y = z, logo x . y . 1 = z.(obs:o 0 é o da soma.)
- Elemento opositor: O fator -1 (menos um) transforma o produto em seu simétrico. Assim, -1 . x = -x e -1 . y = -y, para y diferente de x.
- Fechamento: O produto de dois números reais será sempre um número real.
- Anulação: O fator 0 (zero) anula o produto. Assim, x . 0 = 0, e y . 0 = 0, com x diferente de y.
Na matemática, podemos dizer que a multiplicação é a mais simples formar de agruparmos uma quantidade finita de números.Ao efetuarmos uma multiplicação, chegamos a uma resposta que é chamada de PRODUTO. Na geometria , está relacionada também como uma operação geométrica - a partir de dois segmentos de retas dados, podemos determinar um outro cujo comprimento seja igual ao produto dos dois inciais.
Divisão
Divisão é a operação matemática inversa da multiplicação. O ato de dividir por um elemento de um conjunto só faz sentido quando a multiplicação por aquele elemento for uma função bijetora.
No anel dos números inteiros a hipótese da bijetividade não é satisfeita para o zero, assim, não se define divisão por zero.
PROPRIEDADES IMPORTANTES
As propriedades da divisão são herdadas, via inversão, da multiplicação. Não existe, entretanto, a propriedade de fechamento no conjunto dos números reais, uma vez que a divisão por zero não produz como resultado um número real.
[editar]Nos números inteiros
Os números inteiros não formam um corpo, portanto a divisão (como foi definido) só faz sentido quando o número que vai ser dividido (dividendo[1]) é um múltiplo inteiro do número pelo qual se vai dividir (divisor[1]). Para tratar dos casos em que o dividendo não é um múltiplo do divisor é necessário definirquociente e resto.
Se a e b são dois números inteiros positivos (com 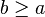 ), o quociente[1] da divisão de a por b é o maior número inteiro q tal que
), o quociente[1] da divisão de a por b é o maior número inteiro q tal que  . O resto[1] da divisão de a por b com quociente q é o número inteiro r tal que
. O resto[1] da divisão de a por b com quociente q é o número inteiro r tal que  .
.
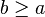 ), o quociente[1] da divisão de a por b é o maior número inteiro q tal que
), o quociente[1] da divisão de a por b é o maior número inteiro q tal que  . O resto[1] da divisão de a por b com quociente q é o número inteiro r tal que
. O resto[1] da divisão de a por b com quociente q é o número inteiro r tal que  .
.
A noção de resto no anel dos números inteiros está intimamente conectada com a noção de congruência.
[editar]Nos números racionais, reais e em outros corpos
Por se tratarem de corpos, a divisão nesse caso fica reduzida a multiplicação pelo inverso.
Por um exemplo, para dividirmos um número racional  por
por 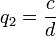 (com as hipóteses de que a,b,c e d sejam inteiros e que b,c e d sejam diferentes de zero) devemos prosseguir da seguinte forma
(com as hipóteses de que a,b,c e d sejam inteiros e que b,c e d sejam diferentes de zero) devemos prosseguir da seguinte forma
 por
por 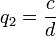 (com as hipóteses de que a,b,c e d sejam inteiros e que b,c e d sejam diferentes de zero) devemos prosseguir da seguinte forma
(com as hipóteses de que a,b,c e d sejam inteiros e que b,c e d sejam diferentes de zero) devemos prosseguir da seguinte forma
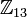
Em (grupo multiplicativo dos inteiros módulo 13), que também é um corpo, a divisão de 7 por 5 se daria da seguinte forma:
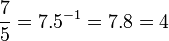
Equação
Em matemática, uma equação é uma afirmação que estabelece uma igualdade entre duas expressões matemáticas.[1][2]
São exemplos de equações as seguintes igualdades:
Nesses exemplos, as letras 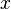 e
e  são as incógnitas de suas equações. A incógnita de uma equação é o número desconhecido que se quer descobrir.
são as incógnitas de suas equações. A incógnita de uma equação é o número desconhecido que se quer descobrir.
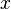 e
e  são as incógnitas de suas equações. A incógnita de uma equação é o número desconhecido que se quer descobrir.
são as incógnitas de suas equações. A incógnita de uma equação é o número desconhecido que se quer descobrir.
A equação  pode ser interpretada como uma pergunta: "qual o número que somado com 8 dá 15?". Não é necessário nenhum método ou fórmula para encontrar o valor de
pode ser interpretada como uma pergunta: "qual o número que somado com 8 dá 15?". Não é necessário nenhum método ou fórmula para encontrar o valor de 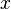 nesse caso: basta pensar um pouco para se chegar ao resultado
nesse caso: basta pensar um pouco para se chegar ao resultado  .
.
 pode ser interpretada como uma pergunta: "qual o número que somado com 8 dá 15?". Não é necessário nenhum método ou fórmula para encontrar o valor de
pode ser interpretada como uma pergunta: "qual o número que somado com 8 dá 15?". Não é necessário nenhum método ou fórmula para encontrar o valor de 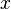 nesse caso: basta pensar um pouco para se chegar ao resultado
nesse caso: basta pensar um pouco para se chegar ao resultado  .
.
Resolver uma equação é encontrar todos os valores possíveis para a incógnita que tornem a igualdade verdadeira.[3] As equações mostradas nos exemplos acima podem ser interpretadas e resolvidas facilmente: o número que subtraído de 10 é igual a 4 é 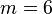 ; o número que, ao ser multiplicado por 3, resulta em 18 é
; o número que, ao ser multiplicado por 3, resulta em 18 é  .
.
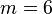 ; o número que, ao ser multiplicado por 3, resulta em 18 é
; o número que, ao ser multiplicado por 3, resulta em 18 é  .
.
Uma solução da equação também é chamada raiz da equação.
Algumas equações matemáticas descrevem, na verdade, identidades matemáticas, isto é, afirmações que são verdadeiras para todos os valores de 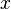 ,[2] como nos exemplos:
,[2] como nos exemplos:
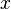 ,[2] como nos exemplos:
,[2] como nos exemplos:
Entretanto, uma equação pode ter apenas alguns valores para os quais ela se torna verdadeira. Nesse caso, ela deve ser resolvida para se encontrar os valores possíveis para as incógnitas. Por exemplo, considere a equação:
Ela é satisfeita para exatamente dois valores de 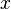 , a saber,
, a saber,  e
e  .
.
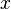 , a saber,
, a saber,  e
e  .
.
Em geral, os matemáticos reservam a palavra equação exclusivamente para igualdades que não são identidades. A distinção entre esses dois conceitos pode ser bastante sutil. Por exemplo:
é uma identidade, mas:
é uma equação cujas soluções são  e
e  .
.
 e
e  .
.
Em geral, é possível perceber se se trata de uma identidade ou de uma equação pelo contexto em que a igualdade se encontra. Em alguns casos, na identidade, o sinal de igualdade (=) é trocado pelo sinal  .
.
 .
.
Equação do segundo grau
Em matemática, uma equação quadrática ou equação do segundo grau é uma equação polinomial de grau dois. A forma geral deste tipo de equação é:

onde x é uma variável, e a, b e c são constantes, das quais a ≠ 0 (caso contrário, a equação torna-se linear). As constantes a, b e c, são chamadas respectivamente de coeficiente quadrático, coeficiente linear e coeficiente constante ou termo livre. A variável x representa um valor a ser determinado, e também é chamada de incógnita. O termo "quadrático" vem de quadratus, que em latim significa quadrado. Equações quadráticas podem ser resolvidas através da fatoração, do completamento de quadrados, do uso de gráficos, da aplicação do método de Newton ou do uso de uma fórmula (apresentada abaixo). Um uso frequente das equações do segundo grau é no cálculo das trajetórias de projéteis em movimento.
A equação quadrática é, antes de tudo, um polinômio do segundo grau, isto é, tem como termo de maior grau (valor do expoente mais alto) um termo de expoente 2. A definição "a diferente de zero" é o que caracteriza a equação de segundo grau, visto que a incógnita  é diretamente multiplicada pelo coeficiente a, e portanto se a fosse igual a zero, anular-se-ia o
é diretamente multiplicada pelo coeficiente a, e portanto se a fosse igual a zero, anular-se-ia o  , e assim a equação passaria a ser linear.
, e assim a equação passaria a ser linear.
 é diretamente multiplicada pelo coeficiente a, e portanto se a fosse igual a zero, anular-se-ia o
é diretamente multiplicada pelo coeficiente a, e portanto se a fosse igual a zero, anular-se-ia o  , e assim a equação passaria a ser linear.
, e assim a equação passaria a ser linear.
No século XII, o matemático Bhaskara Akaria se dispôs a resolver esta equação e publicar ao mundo suas descobertas. O maior problema dos matemáticos que tentavam achar valores para equação era o fato de haver um x de expoente 2 junto a um x de expoente 1. Sabiamente, Bhaskara aplicou princípios básicos, porém inteligentes, para finalmente achar um valor definitivo de x. A partir da descoberta de sua fórmula, diversas outras fórmulas se derivaram, como as fórmulas de Soma e Produto, Relações entre as Raízes ou os valores dos Vértices de uma função quadrática.
Paralela à evolução dos estudos matemáticos da equação de segundo grau, cresceu também sua representação gráfica a chamada função quadrática. Nela, foi possível nitidamente, observar que há sempre um cume, valor máximo que a incógnita pode ter (chamada de Vértice), assim como a direção para a qual os valores crescem, etc. O conhecimento já guardado das funções, quando aplicados na equação quadrática, facilitaram demasiadamente os estudos de matemáticos ao longo da história.
Durante longo tempo diversos estudiosos tentaram achar uma solução para x nesta equação, complicado por haver um termo ao quadrado e o mesmo de primeiro grau.[carece de fontes] Assim, a fórmula de Bhaskara utiliza um método inteligente, unindo pura e simplesmente, uma fatoração de um polinômio para conseguir pôr apenas uma incógnita x no caso e assim, achar um valor definitivo[carece de fontes]:
Se 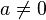 então:
então:
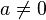 então:
então: |
Logo, tem-se, por definição de módulo, que:
Se  | Se  |
|---|---|
 |  |
Portanto,
 |
Ou:
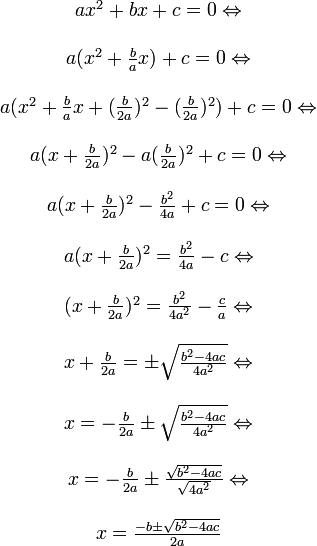 |
Mais:
- Equação do terceiro grau
- Equação do quarto grau – Wikipédia, a enciclopédia livre
- Equação do quinto grau – Wikipédia, a enciclopédia livre
Equação do pêndulo
A matemática envolvida em um simples pêndulo pode ser bastante complexa. O estudo da equação do pêndulo envolve sobretudo a teoria dasequações diferenciais e das integrais elípticas.
A EQUAÇÃO DO MOVIMENTO
Um pêndulo gravitacional simples ideal envolve as seguintes hipóteses:
- A massa pendular está concentrada apenas no elemento oscilante;
- A haste pendular não possui massa, é inextensível e inflexível;
- O movimento pendular acontece em apenas duas dimensões (num plano);
- O movimento pendular é conservativo (não há força de atrito).
A equação diferencial ordinária que governa o movimento do pêndulo é a chamada "equação de Mathieu":
onde  é a aceleração da gravidade e
é a aceleração da gravidade e  é o comprimento da haste.
é o comprimento da haste.
 é a aceleração da gravidade e
é a aceleração da gravidade e  é o comprimento da haste.
é o comprimento da haste.
Pode-se reescrever esta equação na forma usual de sistemas dinâmicos:
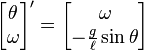
CONSERVAÇÃO DE ENERGIA
Podemos encontrar uma lei de conservação para o movimento do pêndulo, integrando a equação de Mathieu multiplicada por e observando a igualdade
e observando a igualdade  :onde C é a constante de integração que depende das condições iniciais.Podemos reorganizar esta expressão da seguinte forma:Quando
:onde C é a constante de integração que depende das condições iniciais.Podemos reorganizar esta expressão da seguinte forma:Quando pertence ao intervalo
pertence ao intervalo ![[-1,+1]\,](http://upload.wikimedia.org/wikipedia/pt/math/3/2/5/325e5c0940c45fb45285202b0971fcce.png) , existe um ângulo
, existe um ângulo 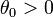 tal que
tal que  e mais uma vez podemos reescrever a lei de conservação da seguinte forma:Aqui
e mais uma vez podemos reescrever a lei de conservação da seguinte forma:Aqui é o ponto de repouso do pêndulo e, portanto, seu o movimento fica restrito ao intervalo
é o ponto de repouso do pêndulo e, portanto, seu o movimento fica restrito ao intervalo ![\theta\in [-\theta_0,\theta_0]\,](http://upload.wikimedia.org/wikipedia/pt/math/f/9/9/f995199462a239d2ea3232c9060d51ac.png)
se não achou o que queria pesa pelos comentários. :D




![x \cdot y = \begin{matrix} \underbrace{y+y+\cdots+y}\\{x}\\[-4ex] \end{matrix}](http://upload.wikimedia.org/wikipedia/pt/math/f/5/a/f5a50bc2e418f83b2798e260770aa8f0.png)
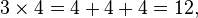
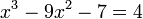

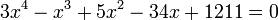







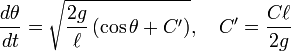







0 comentários:
Postar um comentário